Investigating the Absorption of Radiation in Matter using G-M Counter

 Abstract

In this experiment we will study the process of beta decay, measurements of the shape of beta ray spectrum and determination of beta spectrum end-point energy by graph a kurie or Fermi plot. Also, we will calculate the resolution of the spectrometer by using the internal conversion peaks.

Introduction

The three common decay modes of nuclei (α, β, and γ) were all observed by the early twentieth century. When a nucleus decays, all the conservation laws must be observed: mass-energy, linear momentum, angular momentum, and electric charge. To these laws we add another one for radioactive decay, called the conservation of nucleons. It states that the total number of nucleons (A, the mass number) must be conserved in a low-energy nuclear reaction (say, less than 938 MeV) or decay. Neutrons may be converted into protons, and vice versa, but the total number of nucleons must remain constant.

Radioactive decay may occur for a nucleus when some other combination of the A nucleons has a lower mass. Let the radioactive nucleus ^A X_Z be called the parent and have the mass M (^A X _Z). Two or more products can be produced in the decay. The study of Beta decay as well as Alpha and Gamma signaled the start of the nuclear physics and led to the prediction of the existence of the neutrino.

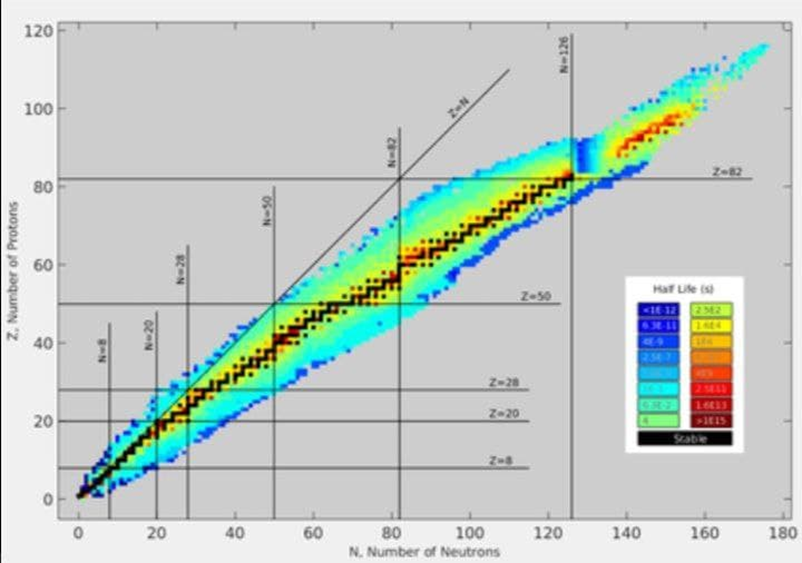
Radioactive decay occurs because some nuclides are not stable. In Figure1 we showed a plot of stable nuclei. In many cases alpha decay leaves the daughter nucleus farther from the line of stability than the parent. Unstable nuclei may move closer to the line of stability by undergoing beta decay. The simplest example of beta decay is the decay of a free neutron.

n   →   P + β^-

Figure 1: A plot of the known nuclides with neutron number N versus proton number Z. The solid points represent stable nuclides, and the shaded area represents unstable nuclei. A smooth line through the solid points would represent the line of stability.

The decay produces two products and we expect to measure a monoenergetic electron spectrum. However, the electron energy spectrum from the beta decay (see Figure 2) shows a continuous energy spectrum up to a maximum energy. This experimental result was a major puzzle for many years. In addition to the strange energy spectrum, there was a problem with spin conservation. In neutron decay, the spin 1/2 neutron cannot decay to two spin 1/2 particles, a proton and an electron. We cannot combine spin 1/2 and 1 to obtain a spin of 0. Both the electron energy spectrum and the spin angular momentum conservation posed major difficulties with our understanding of beta decay.

The correct explanation was proposed in 1930 by Wolfgang Pauli, who suggested that a third particle—later called a neutrino—must also be produced in beta decay. The neutrino, with the symbol ν , has spin quantum number 1/2, charge 0, and carries away the additional energy missing in Figure 2. In Figure 2 an occasional electron is detected with the kinetic energy K _max required to conserve energy, but in the great majority of cases the electron’s kinetic energy is less than K _max. We know that the  neutrino has mass, although it is extremely small. Its energy is almost all kinetic.

The photon cannot be the missing particle because it has spin 1. Pauli’s suggestion seemed to explain the difficulties, and all circumstantial evidence supported the neutrino hypothesis. However, the detection of the elusive neutrino was difficult, and its existence was not proven experimentally until 1956 by C. 

In order to incorporate these features, Fermi formulated a field theory for β decay. The Fermi theory assumes that the β decay of a nucleus proceeds via the β decay of one of the nucleons making up the nucleus. It thus predicted the following basic nuclear β decay processes:

In this experiment the beta ray spectrometer utilizes a magnetic field (B) which deflects the 

particles in a path of known curvature through an angle 180⁰ between two points (the source and the detector) spaced at a distance 2r apart. The 180⁰ point on the trajectory is called the "first order focus" because electrons emitted with small angular deviations from normal tend to be focused at 180⁰.

For most of the beta-decay particles, relativistic relations connecting the momentum and kinetic energy must be used in the calculations, i.e.

Thus if the rest mass of the particle is known, its energy can be deduced from the measured momentum using the spectrometer. An electron with velocity v entering a region where there is a magnetic field B , such that v is perpendicular to  B suffers a magnetic force:

F_M = evB = (mv^²) / r

P = mv = eBr

Combining this equations we get:

The spectrum of 𝜷 decay is continuous, so it cannot be used to calibrate the energy measurements taken by the spectrometer with good precision. Some beta sources produce a mono-energetic spectral line in addition to the continuous beta spectrum. These mono-energetic electrons are due to a transition process known as internal conversion.

The internal conversion arises when one or more nucleons in the nucleus rearrange themselves during a transition from an initial to a final state. The nuclear energy (Ei - Ef) is transferred directly to an atomic electron bound in the atom with an energy Ex where x is the atomic shell (K, L, M, … etc.) or emits γ-radiations, because these processes are independent. Fig. 3 shows the spectrum of ¹³⁷Cs which consists of a continuous spectrum and a spectral line. Note the continuous part (due to beta decay) and the monoenergetic lines (due to "internal conversion" resulting in the ejection of an electron from the K and L shells). Usually the spectrometer is calibrated and its resolution is measured by the study of the internal conversion electron spectra. The conversion electron energies Ee for K and L shell of 137Cs are 624.2 keV and 656.0 keV [3], respectively

Methodology

Apparatus:

1. Beta ray source 137Cs.

2. End window Geiger counter.

3. Scaler to count the emitted beta particles.

4. Rotary vacuum pump to evacuate the chamber housing the source and the counter.

5. Electromagnet with its power supply.

Procedure:

1. Use the rotary pump to evacuate the vacuum chamber in order to reduce the collisions between the b particles and the air molecules.

2. Be sure that the end window Geiger counter is operated within its plateau region. Higher voltages will damage the counter. Note: Do not exceed 500 volts on the Geiger counter used in this experiment.

3. With no magnet current flowing, take the background counting rate for a period of at least 15 minutes.

4. Raise the magnet current gradually and take the number of the counts per 3 minutes N(p) for different values of the magnetic fields B (or the magnet current I).

5. Make sure that you continue increasing the magnet current until you obtain a broad peak and a sharp peak.

Data Analysis

Calculate Pe and Ee for each value of the magnetic field B.

the background value corresponds to I=0  the table below shows the corrected count rate number which is the counts number taken every 300 sec – the background value .

to calculate the value of B  use this equation

B(mT) = -23.88I^2 + 19.54I^2 + 147I + 1.253

To convert it to Gauss use the relation:

1Gauss=10^-4

R=1.5inch=3.81cm

current(A)	N/300sec	N	B (GAUSS)	B*r(Gauss.cm)
0	120	0	12.53	47.7393
0.02	172	52	42.00625	160.0438125
0.04	149	29	71.62736	272.9002416
0.06	166	46	101.62736	387.2002416
0.08	168	48	131.2583	500.094123
0.1	195	75	161.2452	614.344212
0.12	264	144	191.3311	728.971491
0.14	345	225	221.5046	843.932526
0.16	338	218	251.7541	959.183121
0.18	388	268	282.0683	1074.680223
0.2	425	305	312.4356	1190.379636
0.22	444	324	342.8446	1306.237926
0.24	458	338	373.2839	1422.211659
0.26	480	360	403.7419	1538.256639
0.28	417	297	434.2072	1654.329432
0.3	450	330	464.6684	1770.386604
0.32	429	309	495.114	1886.38434
0.34	403	283	525.5324	2002.278444
0.36	403	283	555.9124	2118.026244
0.38	360	240	586.2423	2233.583163
0.4	324	204	616.5108	2348.906148
0.42	342	222	646.7063	2463.951003
0.44	292	172	676.8175	2578.674675
0.46	239	119	706.8328	2693.032968
0.48	191	71	736.7408	2806.982448
0.5	170	50	766.53	2920.4793
0.51	173	53	781.3765	2977.044465
0.52	160	40	796.189	3033.48009
0.53	129	9	810.966	3089.78046
0.54	175	55	825.7062	3145.940622
0.55	199	79	840.4082	3201.955242
0.56	389	269	855.0703	3257.817843
0.57	461	341	869.6914	3313.524234
0.58	541	421	884.2698	3369.067938
0.59	512	392	898.8042	3424.444002
0.6	449	329	913.2932	3479.647092
0.61	331	211	927.7353	3534.671493
0.62	178	58	942.129	3589.51149
0.63	163	53	956.373	3643.78113
0.64	155	35	970.7695	3698.631795
0.65	136	16	985.0061	3752.873241
0.66	141	21	1232.1227	4694.387487

Read alsoDiffraction Grating Spectrometry Experiment

Read alsoElectron Diffraction Experiment

Read alsoBeta Spectroscopy Experiment

Read alsoPhoton Polarization Experiment

This graph represents the beta spectrum , it's a continuous spectrum with two monochromatic energy  lines ,k and L shells resulting from internal conversion electrons. The first peak corresponding to k shell electrons occurred at current 0.58 A , the second peak corresponding to L-shell electrons occurred at 0.60 A .

N	P	Ee(Mev)		T(Mev)	p^2	(n/p^2)^1/2
0	0.014319	0.511201	0		0.000205	0
52	0.048004	0.51325	0.00225		0.002304	150.231
29	0.081854	0.517514	0.006514		0.0067	65.79025
46	0.115856	0.523969	0.012969		0.013423	58.54018
48	0.149998	0.53256	0.02156		0.022499	46.18904
75	0.184266	0.543208	0.032208		0.033954	46.9986
144	0.218648	0.555813	0.044813		0.047807	54.8827
225	0.253129	0.570259	0.059259		0.064074	59.2584
218	0.287697	0.586422	0.075422		0.08277	51.3206
268	0.32234	0.604172	0.093172		0.103903	50.78709
305	0.357042	0.623378	0.112378		0.127479	154.6787
324	0.391793	0.643912	0.132912		0.153502	45.9425
338	0.426578	0.66565	0.15465		0.181969	43.0982
360	0.461385	0.688474	0.177474		0.212876	41.1232
297	0.4962	0.712275	0.201275		0.246214	34.7313
330	0.53101	0.724508	0.213508		0.281972	34.21007
309	0.565802	0.736948	0.225938		0.320132	31.0681
283	0.600563	0.7624	0.2514		0.360676	28.0113
283	0.635281	0.788541	0.277541		0.403582	26.4805
240	0.669941	0.815293	0.304293		0.448821	23.1243
204	0.704531	0.842581	0.331581		0.496364	20.2728
222	0.739038	0.88437	0.37337		0.546177	20.1608
172	0.773448	0.912712	0.401712		0.598222	16.9563
119	0.807784	0.941376	0.430376		0.652515	13.5044
71	0.841926	0.970311	0.459311		0.708839	10.0081
50	0.875969	0.999471	0.488471		0.767322	8.0722
53	0.892935	1.014121	0.503121		0.797333	8.153
40	0.909862	1.028812	0.517812		0.827849	6.9511
9	0.926749	1.043537	0.532537		0.858864	3.2371
55	0.943594	1.058293	0.547293		0.89037	7.8595
79	0.960394	1.073075	0.562075		0.922357	9.2547
269	0.97715	1.087878	0.576878		0.954822	16.7847
341	0.993858	1.102698	0.591698		0.987754	18.5803
421	1.010518	1.117531	0.606531		1.021147	20.3047
392	1.027128	1.132373	0.621373		1.054992	19.276
329	1.043685	1.147219	0.636219		1.089278	17.3791
211	1.060185	1.162067	0.651067		1.123992	13.7012
58	1.076638	1.176912	0.665912		1.159149	7.0736
53	1.09303	1.191751	0.680751		1.194715	6.6604
35	1.109363	1.20658	0.69558		1.230686	5.3328
16	1.125637	1.221396	0.710396		1.267059	3.5535

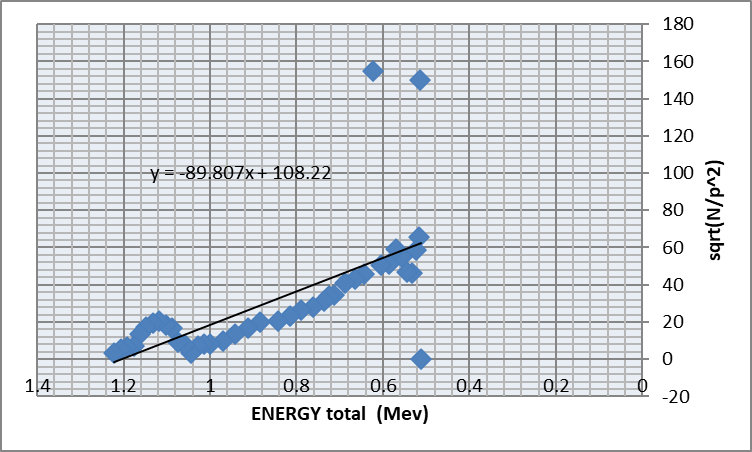
Figure 2: Kurie plot to determine the end point energy (max. energy of beta particle ).

End point energy = x-intercept = 108.22 / 89.807 = 1.205 MeV

T0 =Etotal-0.511=0.694 Mev

Accepted value of T0 =0.514             Mev 

To estimate the true value our slope and y-intercept we use the least square method:

	Ee(Mev)	(n/p^2)^1/2	x*y	x^2	(y-a-bx)^2
	0.511201	0	0	0.261326	3882.607
	0.51325	150.231	77.10606	0.263426	7762.393
	0.517514	65.79025	34.04738	0.267821	16.37521
	0.523969	58.54018	30.67324	0.274544	6.883991
	0.53256	46.18904	24.59844	0.28362	201.735
	0.543208	46.9986	25.53002	0.295075	154.6919
	0.555813	54.8827	30.50452	0.308928	11.70599
	0.570259	59.2584	33.79264	0.325195	5.069928
	0.586422	51.3206	30.09553	0.343891	17.93183
	0.604172	50.78709	30.68414	0.365024	10.0745
	0.623378	154.6787	96.4233	0.3886	10494.45
	0.643912	45.9425	29.58293	0.414623	19.79979
	0.66565	43.0982	28.68832	0.44309	28.53451
	0.688474	41.1232	28.31225	0.473996	27.74145
	0.712275	34.7313	24.73824	0.507336	90.65742
	0.724508	34.21007	24.78547	0.524912	79.99585
	0.736948	31.0681	22.89557	0.543092	120.3148
	0.7624	28.0113	21.35582	0.581254	137.8239
	0.788541	26.4805	20.88096	0.621797	119.3119
	0.815293	23.1243	18.85308	0.664703	141.0556
	0.842581	20.2728	17.08148	0.709943	150.7377
	0.88437	20.1608	17.82961	0.78211	74.59057
	0.912712	16.9563	15.47622	0.833043	86.4114
	0.941376	13.5044	12.71272	0.886189	103.499
	0.970311	10.0081	9.71097	0.941503	122.571
	0.999471	8.0722	8.06793	0.998942	107.9169
	1.014121	8.153	8.268129	1.028441	80.8531
	1.028812	6.9511	7.151375	1.058454	78.75463
	1.043537	3.2371	3.378034	1.088969	126.9221
	1.058293	7.8595	8.317654	1.119984	28.28517
	1.073075	9.2547	9.930987	1.15149	6.737417
	1.087878	16.7847	18.25971	1.183479	39.23468
	1.102698	18.5803	20.48846	1.215943	88.17772
	1.117531	20.3047	22.69113	1.248876	154.923
	1.132373	19.276	21.82762	1.282269	162.5886
	1.147219	17.3791	19.93763	1.316111	148.5326
	1.162067	13.7012	15.92171	1.3504	96.88369
	1.176912	7.0736	8.325005	1.385122	20.68918
	1.191751	6.6604	7.937538	1.42027	29.89883
	1.20658	5.3328	6.43445	1.455835	29.94421
	1.221396	3.5535	4.340231	1.491808	25.23465
sum	34.93481	1299.542	897.6365	32.10143	25092.54

a is the intercept and b is the slope .

The error in a and b using these equations:

For resolution computations and from internal conversion spectrum :

I A	N/I(1/A)
0.53	243.3962
0.54	324.0741
0.55	361.8182
0.56	694.6429
0.57	808.7719
0.58	932.7586
0.59	867.7966
0.6	748.3333
0.61	542.623
0.62	287.0968
0.63	258.7302
0.64	242.1875

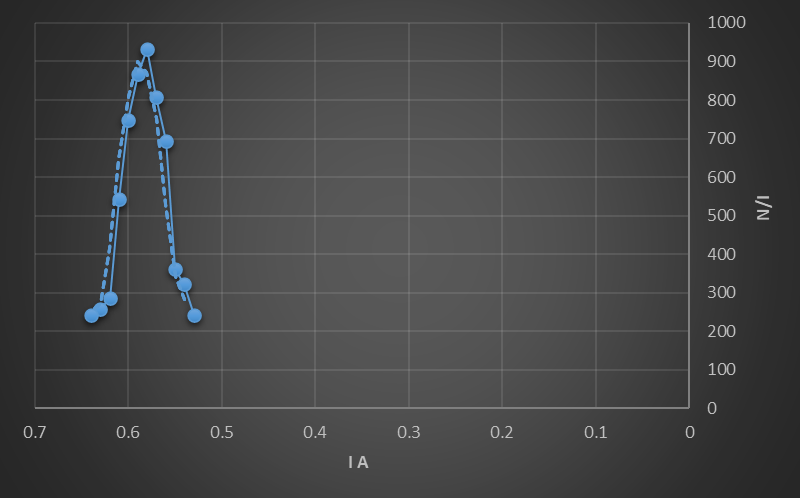
From the graph we can obtain the following information :

(N / Imax)  = 932.75 (1  /A)

Imax = 0.58 A

Height = (1/√2)(N/Imax) = 659.5538 (1/A)

 The half max.=329.7769(1/A) 

∆I at half max. value =(0.62-0.54)= 0.08A 

R = ∆I/I =0.1379

Conclusion

* The beta particles are high energy, high speed electrons or positrons that are ejected from nucleus by some radio nuclei.

* Normally beta decay occurs in nuclei that have too many neutrons to achieve stability. 

*We calculated the kinetic energy of electrons with percentage error= 35.01 %

* We calculated the resolution of the spectrometer and obtained R=0.1379.

References

1- Arthur Beiser; Concepts of Modern Physics, Sixth Edition.

2- Manual of the advanced practical physics 5.

3- Modern Physics, For Scientists and Engineers, Fourth Edition, Stephen T. Thornton.

4- https://wanda.fiu.edu/boeglinw/courses/Modern_lab_manual3/_images/Sr90_decay.png