Investigating the Absorption of Radiation in Matter using G-M Counter

 

Abstract

In this experiment, we shall investigate the wave nature of moving electrons, and interference of electron waves diffracted by polycrystalline layers of graphite. The bright rings produced by interference of electron waves will be used to determine the d-spacing values characteristic of the graphite crystal structure.

Introduction

It was hypothesized in a Ph.D. thesis provided by de Broglie that moving particles are associated with the propagation of waves. The wave length of a particle moving with momentum p is given by equ.1. where h is Planck’s constant. The wave nature of moving electrons was later demonstrated by experimental work of Davisson and Germer.  When parallel rays are incident on a set of scattering atomic planes in a crystal, they are reflected by these planes. Constructive interference is then observed in particular directions, forming a spot on a screen. The angle of scattering in the direction of the spot is determined by Bragg’s law equ.2 , see Fig.1.

Figure 1: Bragg’s law

Here ɵ is the angle between the incident or reflected rays and the scattering lanes. The scattering angle (between the incidence and scattering directions) is 2θ. Usually, the first order reflection (n = 1) is dominant, and higher order reflections are weak. 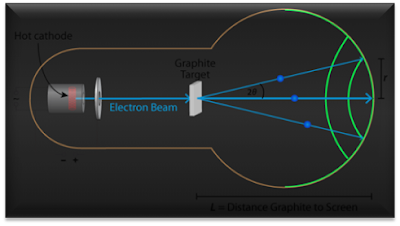If we have a polycrystalline sample, with crystal planes oriented randomly in space, a ring is observed as a consequence of constructive interference of waves scattered from a given set of planes. Fig. 2 shows the diffraction process in the electron diffraction tube of radius R, and one of the observed rings of radius r on the screen.

Figure 2: Diffraction ring due to constructive interference of electron waves
scattered by a polycrystalline sample.

Graphite Structure

Graphite crystal consists of layers of carbon atoms arranged at the vertices of hexagons, each layer having a honeycomb 2-dimensinal arrangement as in Fig. (3). Atoms in the same layer are boded covalently, while different layers are attracted to each other by van der Waal’s forces. The nearest neighbor distance between two atoms in a layer is 1.42 Å, while the c-axis length (perpendicular to the layers) is 6.88 Å. The first two sets of planes with their respective separations are shown Fig. 3 &4. These separations can be easily calculated from the geometry, and are given by equ.7 and equ.8.

Figure 3 &4: Honeycomb arrangement of carbon atoms in a graphite layer.

Methodology

1. Connect the diffraction tube to the power supplies, and switch on the power. Increase the accelerating voltage up to 4 kV until two well defined rings are observed on the fluorescent screen on the tube wall.

2. Measure the outer and inner diameters of each ring using a vernier caliper, and tabulate your results.

3. Repeat the above procedure for accelerating voltages up to 10 kV (step of 0.5 kV). Tabulate your results.

4. For high accelerating voltages, you may observe other rings in addition to the main two rings mentioned above. Measure and tabulate their diameters as before.

Formalism

The wave length of a particle moving with momentum p , where h is Planck’s constant.

Bragg’s law:

2𝑑𝑠𝑖𝑛𝜃 = 𝑛𝜆 ………………… (2)

𝑟 = 𝑅𝑠𝑖𝑛(4𝜃)  ………………. (3)

𝑟 = 4𝑅𝑠𝑖𝑛𝜃  ………………………. (4)

𝑑1 = 1.42(1 + sin(30)) = 2.13 Å  ……..(7)

𝑑2 = 1.42 sin(60) = 1.23 Å  …………...(8)

Data Analysis

V (KV)	d 1( in) (cm)	d 1 (out)(cm)	d 2 (in) (cm)	d 2 (out)(cm)	Average diameter (in) (cm)	Average diameter (out) (cm)
4	2.05	2.66	3.75	4.53	2.355	4.140
4.5	1.94	2.46	3.52	4.30	2.220	3.911
5	1.96	2.36	3.46	4.20	2.160	3.832
5.5	1.85	2.19	3.20	3.75	2.020	3.475
6	1.74	2.01	3.06	3.50	1.870	3.280
6.5	1.70	1.99	3.00	3.35	1.845	3.175
7	1.62	1.90	2.90	3.20	1.760	3.050
7.5	1.51	1.70	2.74	3.19	1.600	3.963
8	1.48	1.67	2.70	3.02	1.570	3.861
8.5	1.40	1.63	2.60	2.90	1.515	3.750
9	1.39	1.61	2.60	3.10	1.500	2.851
9.5	1.30	1.53	2.57	3.10	1.410	2.834
10	1.28	1.57	2.50	3.00	1.420	2.752

Using the value for the tube radius R = 6.5 cm, the radii of the rings, and the equation:

𝑟 = 𝑅𝑠𝑖𝑛(4𝜃) Where r is the radius of the ring

We can calculate the range of the angle θ

And by using the equation:

We can calculate the wavelength for each accelerating voltage. The results are in the table in the following page.

r 1	r 2	θ1	θ2	𝜆(A m)
1.17	2.071	2.579	4.568	0.193848
1.10	1.955	2.424	4.3122	0.182761
1.08	1.915	2.380	4.2238	0.173383
1.01	1.737	2.226	3.830	0.165314
0.93	1.642	2.049	3.620	0.158276
0.92	1.587	2.027	3.499	0.152067
0.88	1.525	1.939	3.3625	0.146535
0.80	1.482	1.763	3.267	0.141566
0.78	1.432	1.719	3.157	0.137071
0.75	1.375	1.652	3.031	0.132978
0.75	1.425	1.652	3.141	0.129232
0.70	1.411	1.542	3.110	0.125785
0.71	1.375	1.564	3.031	0.1226

For the first ring

Radius for the first ring (cm)	Wavelength (A)
1.17	0.193848
1.10	0.182761
1.08	0.173383
1.01	0.165314
0.93	0.158276
0.92	0.152067
0.88	0.146535
0.80	0.141566
0.78	0.137071
0.75	0.132978
0.75	0.129232
0.70	0.125785
0.71	0.1226

Read alsoInvestigating the Absorption of Radiation in Matter using G-M Counter

Read alsoDiffraction Grating Spectrometry Experiment

Read alsoElectron Diffraction Experiment

Read alsoBeta Spectroscopy Experiment

The slope of the straight line = 6.9711 *10^8 m

The relation is linear and direct.

For the second ring

Radius for the second ring (cm)	Wavelength (A)
2.071	0.193848
1.955	0.182761
1.915	0.173383
1.737	0.165314
1.642	0.158276
1.587	0.152067
1.525	0.146535
1.482	0.141566
1.432	0.137071
1.375	0.132978
1.425	0.129232
1.411	0.125785
1.375	0.122600

 

The slope of the straight line = 10.342 *10^8 m

The relation is also linear and direct.

From the slopes in step (3) above, the d- spacing for each ring can be calculated using the equation:

For the first ring, the d-spacing is:

d1 = 1.864A

The real value = 2.14 A

So, the percentage error is:

For the second ring, the d-spacing is:

d2 = 1.211A

 

The real value = 1.2570 A

 

So, the percentage error is:

Discussion 

We increased the retarding potential and measured the inner and the outer diameters of each ring, then we calculated the radius and the range of the angle θ using the equation: r = R Sin (θ), where R is the radius of the tube. We also calculated the wavelength for each accelerating voltage using the equation:

 

Then, we plotted the ring radius versus the wavelength for the two rings and determined the slope of the straight lines.

For the first ring, the slope equals 6.9711 *10^8 m

For the second ring, the slope equals 10.342 *10^8 m

The percentage errors was kind of acceptable,  for d₁ the real value was 2.14  , we found it to be 1.864 , that makes the percentage error 12.89%. For the d₂ the real value was 1.2570, but  ours was 1.211 , so the percentage error is 0.36%.

Conclusion

In this experiment we used an evacuated tube which contain an electron emitter that provides electron beam , it also contains an accelerating anode  to provide a known energy value to the electrons in the beam , crystal targets made of either aluminum or graphite ; and an observing screen for viewing the electron diffraction pattern.

The relation between the radius of the ring and the wavelength of the incident light is linear and direct, which means that as the wavelength of the incident beam increases, the radius of the ring also increases.

The diffraction pattern observed on the screen is a series of concentric rings. This is due to the regular spacing of the carbon atoms in different layers in the graphite. However, since the graphite layers overlay each other in an irregular way the resulting diffraction pattern is circular.

We notice also that when the accelerating voltage is increased, the radius of the rings decreases because the energy of the electron increases. 

References

1- ADVANCED PRACTICAL PHYSICS (0352311), Sami Mahmood, The University of Jordan.